A hierarchy is a structure corresponding to successive partitions of a thing.
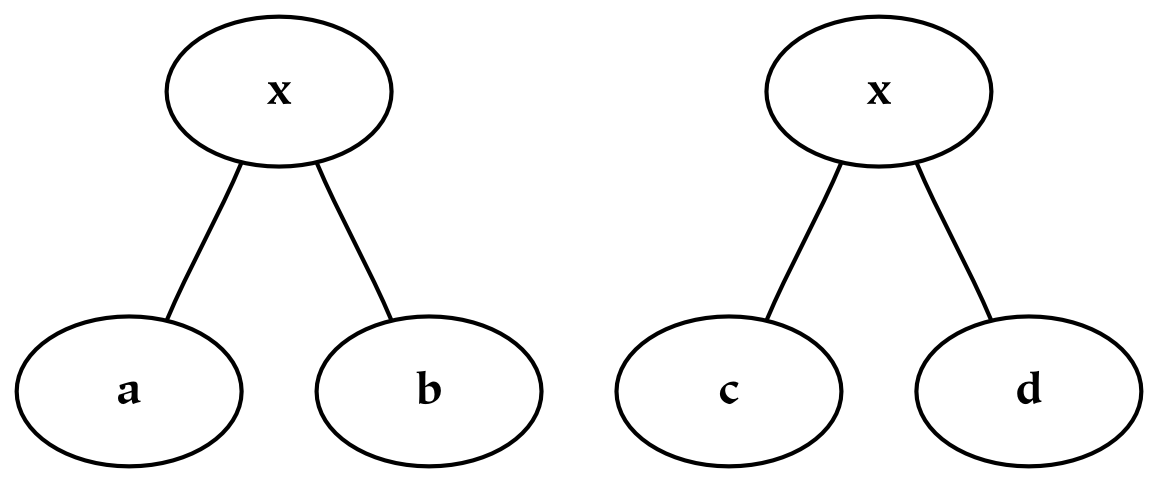
Hierarchies are collections of dimensions (and simultaneously collections of things). They are tree-like structures, or rather root-like structures, since they branch downwards instead of upwards. Hierarchies often represent divisions of a larger whole, where that whole may be a physical, perceptual, or conceptual thing. Graphically, hierarchies can be produced by grafting trees together in a regular way, or appending the branches of one tree to each of the terminal nodes of the other. For example, consider an object, x , which has been divided using two separate dichotomies as follows:
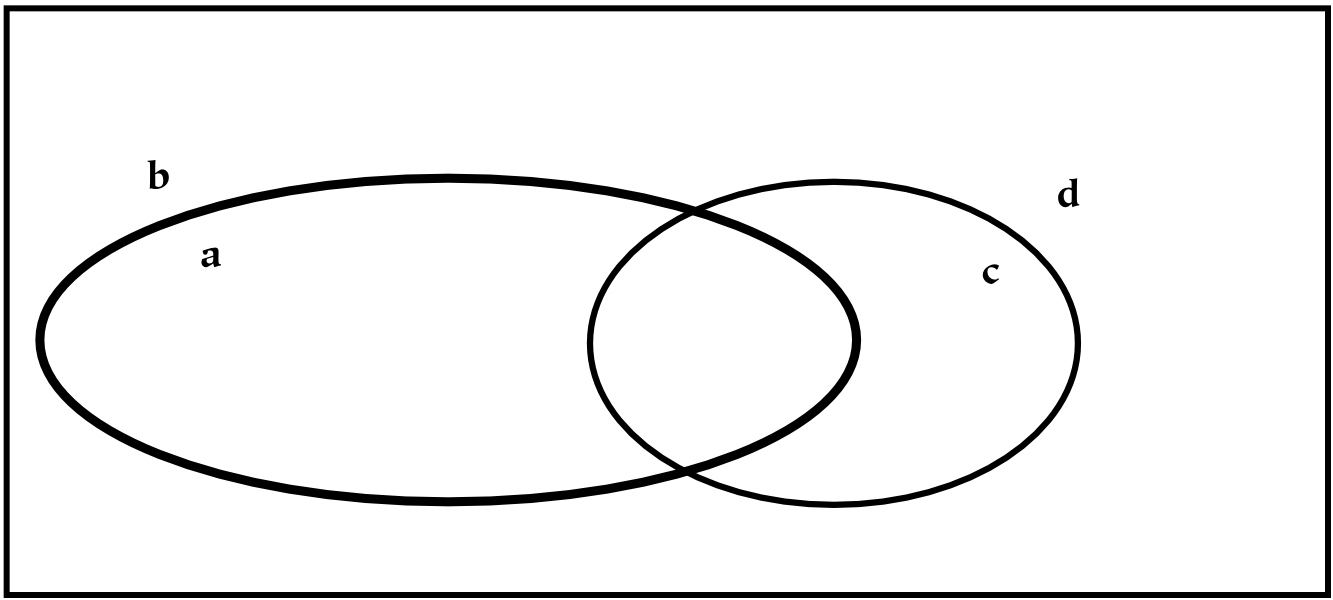
If we wish to combine these two hierarchies, then we may do one of two things. The first possibility is to create a single tree, x , with four children corresponding to (ac, ad, bc, bd). However, this does not preserve the notion of priority: if the division into a/b happens before the division into c/d, this information is lost (or at least, it is no longer preserved graphically).[24] If preserving this information about priority is not required, this tree can also be represented with a Venn diagram, which is essentially a flattened tree diagram. A Venn diagram is shown below, where it has been assumed (graphically) that none of the intersections are empty. The labeling of this diagram is not standard, since here the boundaries are labeled (a/b and c/d). The convention for Venn diagrams is to label the parts, which would yield the parts ac, ad, bc, and bd.
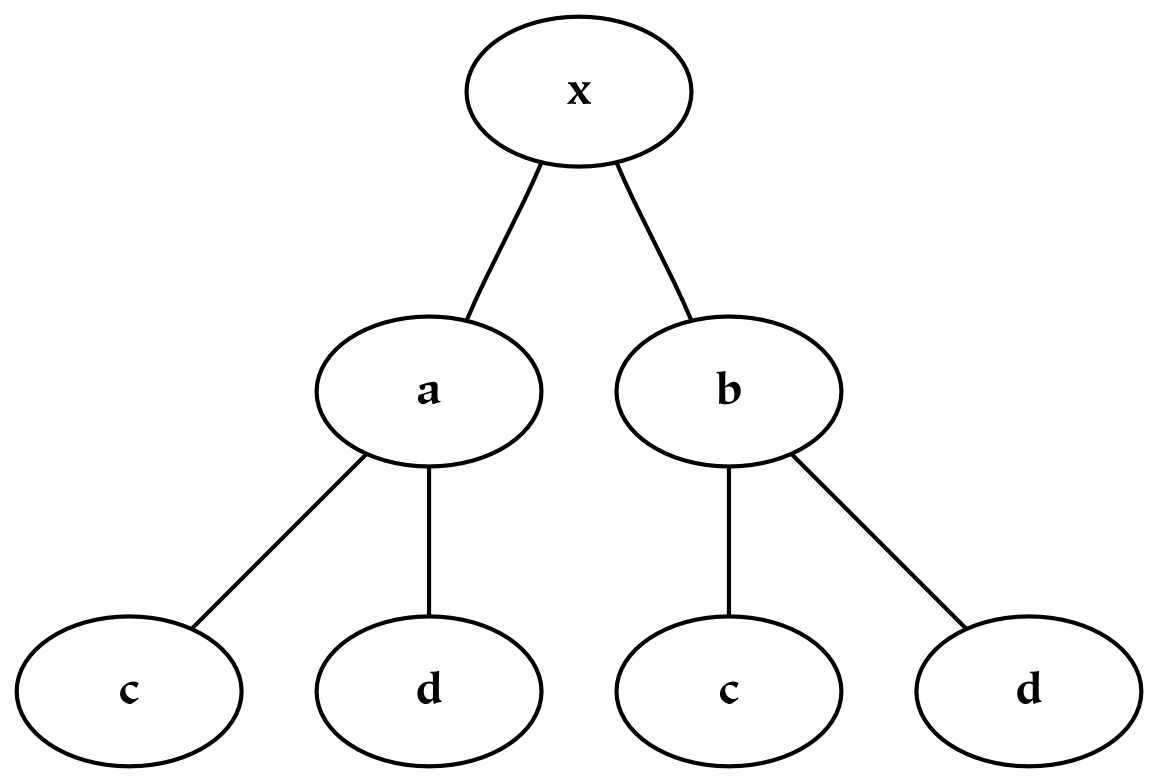
A second possibility for combining the two dimensions is to append the branches of one tree to each of the terminal nodes of the other tree, which in this case results in three layers of nodes. Each path from the root to a terminal node in this tree can be likened to a mathematical cross-product, where pairs are formed by taking one element from each dimension. This sort of combination increases the depth of the hierarchy, and this additional structure allows one to encode additional information: the divisions closer to the root of the tree are prior to those further down.
In some cases, certain of the terminal nodes of the tree will be empty: in those cases, the dimensions were not (entirely) orthogonal. This implies that to some extent, the dimensions encoded the same information. For example, this can happen with the two dichotomies cats/non-cats and animals/non-animals, since there are no cats which are non-animals.[25]
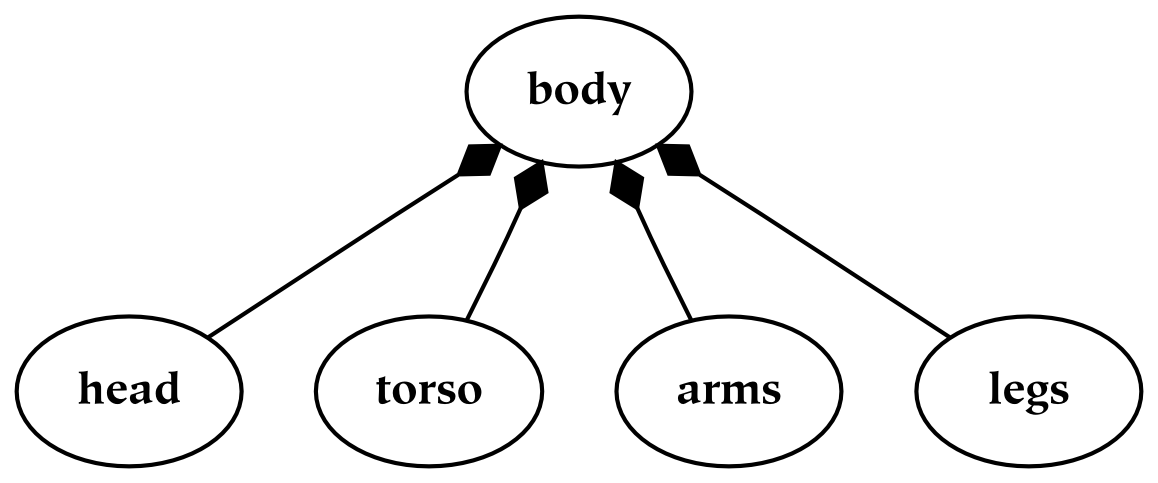
There are two types of common hierarchies which should be carefully distinguished. The first type of hierarchy is known as a meronomy, in which the children are parts of the parent. In the figure below, a meronomy is depicted in which the whole (the entity at the top of the diagram) is a human body, and the parts are the things that compose or constitute the body. This parthood relationship is denoted with shaded diamond arrowheads:
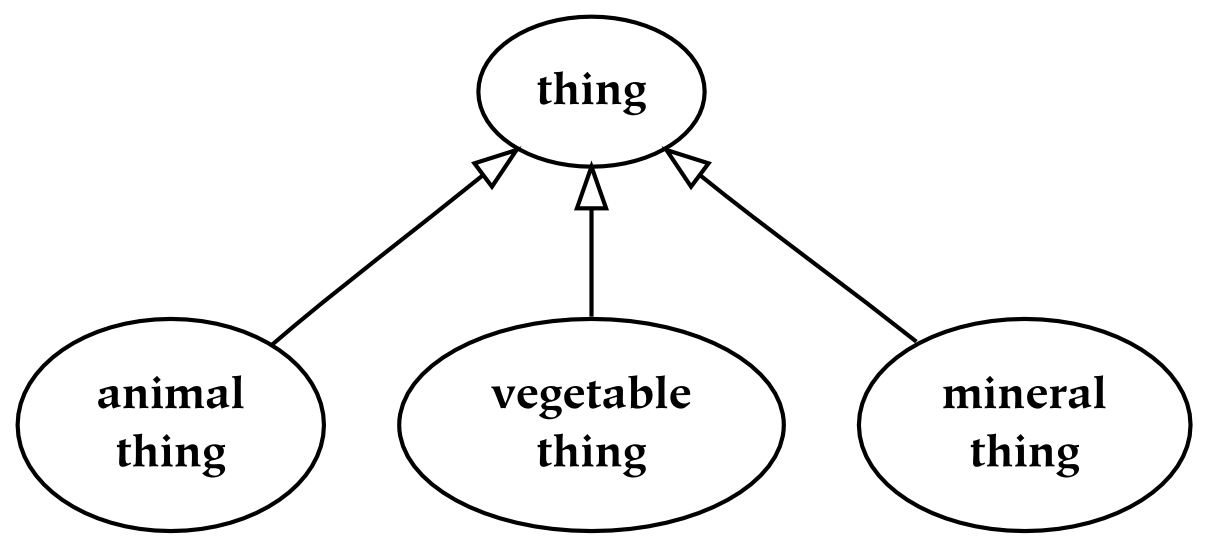
The second type of hierarchy is known as a taxonomy, in which the child things are kinds of the parent things. A taxonomy is similar to a meronomy in that the collection of all the kinds of a thing is a part of the collection of all things; it is different in the way that parts are formed. Perhaps the most important difference is that a taxonomy is typically composed of abstract entities : it is composed of types of things, instead of things themselves. In the following taxonomy, the abstract type “thing” is depicted at the top; it is divided into three types: animal things, vegetable things, and mineral things. To denote this is-a relationship, as opposed to the has-a relationship of meronomies, empty triangle arrowheads are used:
As an example of the difference between meronomies and taxonomies, an animal is-a thing, but a head is-a-part-of-a body (or a body has-a head). However, the collection of all heads is a part of the collection of all bodies, and the collection of all animals is a part of the collection of all things. In both cases, if the hierarchy partitions its whole, then the combination of all the children occupies a space identical with that occupied by the parent.
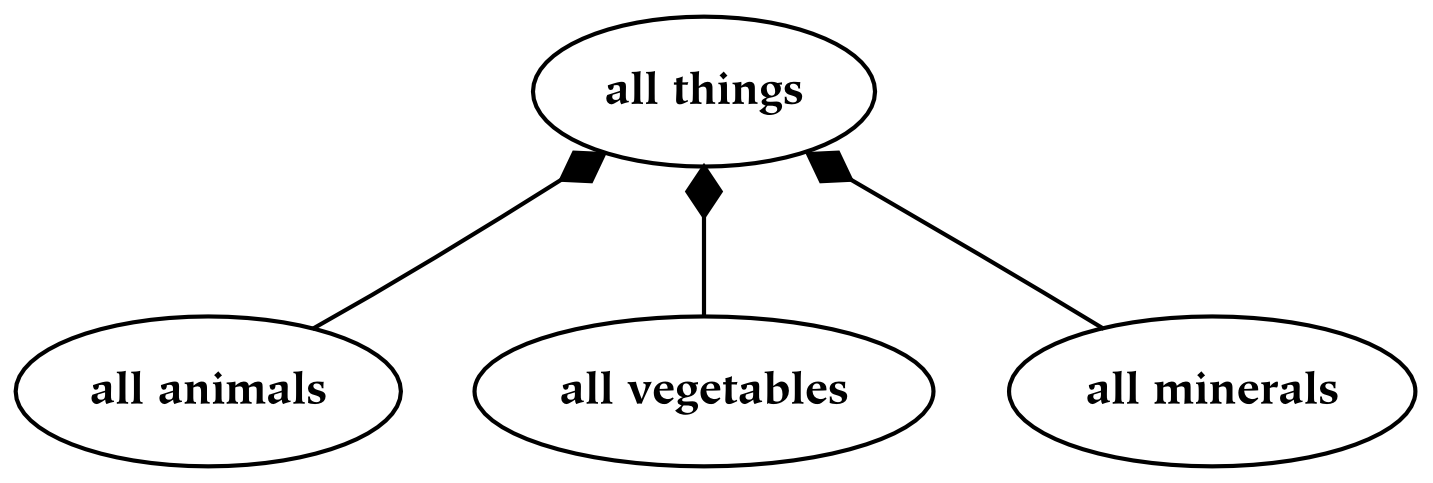
In the following diagram, we represent the extension of the previous (abstract) taxonomy: in other words, the types of the previous taxonomy are represented in this diagram as a set of tokens. An essential difference between this hierarchy and the previous one is that this meronomy consists of nodes which are discontiguous (and plural), while the previous taxonomy consists of nodes which are abstract (and singular). For example, the matter corresponding to “all animals” is distributed in space, as opposed to “animal thing” , which is an abstract type as opposed to a physical entity.
Discontiguous things are often seen to be less real , in some sense, then their connected counterparts: hence, nodes in a meronomy typically represent contiguous quantities. Hence, the previous diagram is often represented with many contiguous nodes, such that all particular animal, vegetable, and mineral things are listed.[26]
As concepts occupy positions in ontological hierarchies with a single root, the notion of ontological priority is introduced.
To refer to the fact that one concept is above another in a hierarchy, we say that it is ontologically prior to the concept which is lower in the hierarchy (the diagrams in this book follow the convention that knowledge starts at the top). Hence, to understand the origins of knowledge, we should understand which categories are primary, and especially which categories are necessarily primary.
The notion that a hierarchy underlies concepts is an extension of what Noam Chomsky called the deep structure of a sentence (the deep structure of a sentence is similar to the tree diagram of a sentence). This deep structure is present in our language, but it is not immediately identifiable (the part of the sentence that is immediately accessible to our perception is known as its surface structure ). The hierarchy in this book is an extension of deep structure: for example, even nouns have a hierarchy associated with them.
The proximity of nodes to the root node in a deep structure is significant: humans learn hierarchies over time, and basic ontological categorization must happen before finer categorical detail can be achieved. With respect to the syntax of a sentence, the primary division (that occurs at the root of the tree) corresponds to the distinction between the noun phrase and the verb phrase. With respect to our vocabularies, the words that we learn first tend to occur at the top: words which are defined in terms of other words often occur further down in the hierarchy (i.e. as compared to the words which are used to define them). Of particular interest are the types of words or phrases which necessarily occur at different ontological levels, as opposed to those that just happen to be learned before others by a given individual. For example, perhaps proper nouns must be learned before count nouns, and will therefore necessarily occur at an earlier ontological level.
Although structure and history are to some degree inexorably intertwined, ontological priority is more about structure than it is time of introduction. For example, suppose someone learned the concept “apple” in terms of the concept “fruit” . In this scenario, “fruit” is learned before “apple” , so for them “fruit” is ontologically prior to “apple” . However, if that person has subsequent direct experience with apples, it is no longer the case that “fruit” is necessarily ontologically prior to “apple” (although it remains the first concept to be learned).
The number of dimensions of a thing is conceptually increased by iterating something along a singleton dimension.
Parts cannot have a dimensionality which is different than the space that contains them. Therefore, increasing the dimensionality of an existing universe by collecting a large number of objects (or reducing the dimensionality by slicing a thing along one of its existing dimensions) is not strictly possible.
However, references to things, understood from within the referential domain (i.e. understood as references instead of as parts ), may have a dimensionality which is different than the dimensionality of the things to which they refer. Further, the references themselves may be collected in a referential space. The effect of doing so is to increase the dimensionality of the things, by abstracting over them.
We will return to the topic of references in future sections, since they have not yet been formally introduced. For now, the increase in dimensionality will be depicted with atoms. Atoms should be conceived of as having a atomic extent in a large number of dimensions (as opposed to a zero size, which is the case for mathematical points). This extent is similar to how one might conceive of a piece of paper: although we may treat it as a two-dimensional object in a large number of contexts, it is actually of a higher dimensionality (otherwise adding pages to a book would not add thickness).
In the figures below, we show the process of adding dimensions to an atomic entity (i.e. one which has no parts). In the first figure, there is simply an atom: it has no extent which can be further subdivided along any dimension. To turn this description around: since it is not possible to sub-divide an atom, an atom does not have any dimensionality.
In Figure 2.11, “A Line: One Dimension”, we iterate the object shown in the first figure, in a direction which is orthogonal to any non-atomic extents already present (which is easy to do for an atom, since it cannot have orientation). In this way, we end up with a line:
This process is repeated to create the second and third dimensions, corresponding to Figure 2.12, “A Plane: Two Dimensions” and Figure 2.13, “A Space: Three Dimensions”. In the first case, many lines, iterated over a new dimension, can be represented as a plane. In the second case, many planes, indexed by a new (orthogonal) dimension, form a three-dimensional space (which may be envisioned as a cube).
The fourth dimension is time. In other words, time may be conceived of as simply another (spatial) dimension. Of course, we seem to move in it in only one direction, so our behavior with respect to it is different. We certainly perceive it differently (if in fact it is perceived, as opposed to being conceived), and we treat it very differently linguistically, but there is no reason to believe that it is of an altogether different nature than the first three spatial dimensions. In fact, it is treated almost identically in modern physical equations dealing with spacetime. In any case, as with the previous dimensions, this novel dimension is introduced by iterating a lower-dimensional object along a new axis, which is orthogonal to those which exist so far.
There are some objects, such as the Necker Cube, which have four spatial dimensions, none of which is a temporal dimension. Such objects are quite difficult to visualize, precisely because of interposing another spatial dimension between the typical three spatial dimensions and the temporal dimension. Perhaps the use of a fourth spatial dimension (instead of the temporal dimension) is desirable because the temporal dimension is perceived in a radically different way than the spatial dimensions. One motivation for not acknowledging time as the fourth (spatial) dimension could be due to the constraints or tendencies of language (and thought). In particular, perhaps there are syntactic constraints that encourage us to extend the dimensionality of noun phrases, rather than add dimensionality to the verb phrase (the analogy between nouns/verbs and space/time is explored in greater detail later in the book).
In any case, despite the fact that the behavior of matter in time is very different that its behavior in space, we will persist in calling time simply the fourth dimension, which downplays its status as a different type of dimension. The ordering of dimensions themselves is a matter of convenience: mapping time to the fourth dimension is an attempt to preserve the order of dimensions that appears most natural (of course, this notion of naturalness may be a bias inherited from the English language, in which the subject comes before the verb).
The depiction of a five-dimensional object is a particularly interesting example of how each successive dimension is produced, because few of us have (at least explicitly) extended our conceptualization of dimensionality that far. Although all of us can picture three dimensions easily, and the intrepid among us can picture four without too much difficulty, the idea of the fifth dimension seems somewhat incomprehensible at best (and at worst, the subject of a bad science fiction novel).
Implicitly, however, we use the fifth dimension all the time. To conceptualize the five-dimensional world, picture this: there is another earth, similar but not exactly the same as ours. It exists at the same place (spatial coordinates) as our earth, and it exists at the same time (temporal coordinate) as our earth. However, we do not trip over the things of that earth: that earth exists in another dimension (i.e. it occupies a different fifth dimensional ordinate).[27] Implicitly, this dimension is used in our language to represent possibility: possible worlds or possible life histories. For example, if we speak of free will, conscious volition is that which is used to choose one or another ordinate on this dimension. As the dimension of possibility, we make use of the fifth dimension all the time; it is not a difficult concept to grasp (even though it is not explicitly spoken of as a spatial dimension). So, if the four dimensions are sufficient to describe a world-line, the fifth dimension allows the representation of multiple world-lines. The introduction of the fifth dimension enables the possibility of discussing possible worlds, so we will refer to the fifth dimension as the dimension of modality.[28]
[24] If we regard the names of the nodes as significant, then this information is still preserved (although it may no longer be inferred from the structure of the tree).
[25] On the other hand, if the nodes at the same level overlap, then they were not the result of a partition. Unless otherwise mentioned, the part hierarchies in this book are partitions.
[26] Diagrammatically, this is indicated with a Kleene star (or an asterisk) next to the node. The Kleene star indicates that there may be a number of instances of the thing that is associated with the star.
[27] Keep in mind that we are talking about conceptual dimensions here: this is how our cognitive landscape is structured. The fifth dimension is a dimension of our thought, regardless of whether it is also a dimension of the physical universe.
[28] Be aware that calling the fifth dimension the dimension of modality, or even talking about the fifth dimension to someone other than a physics geek, is not a common practice.