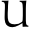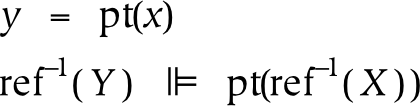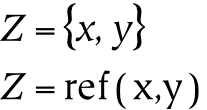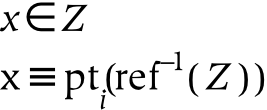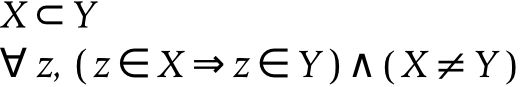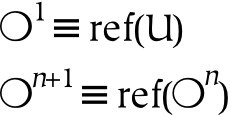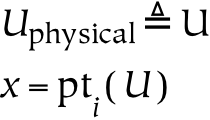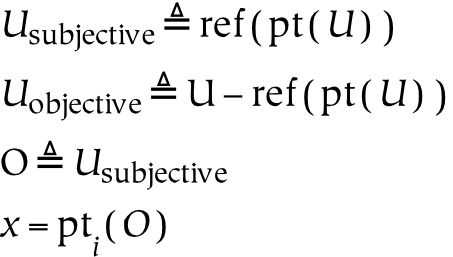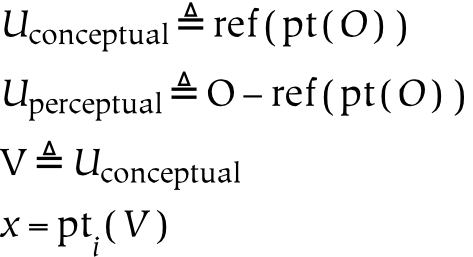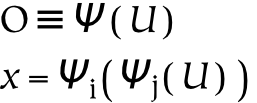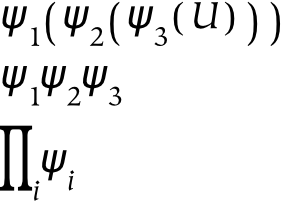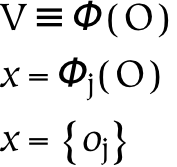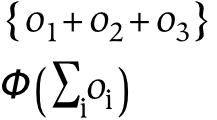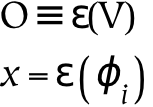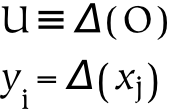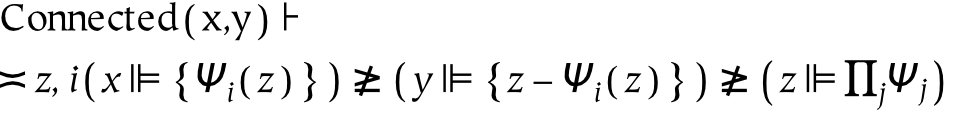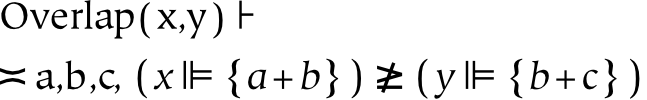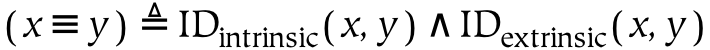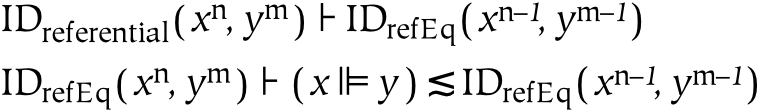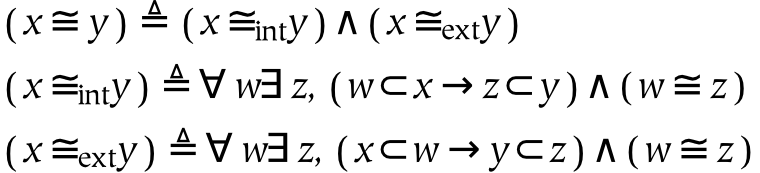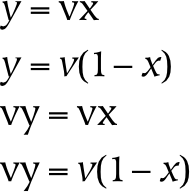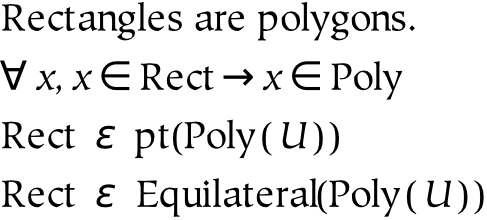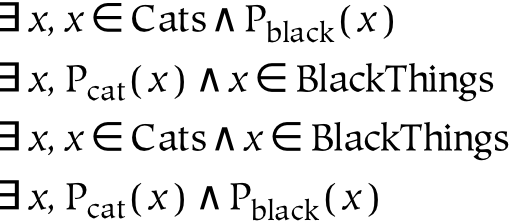Cognitive Set Theory is a formal description of cognition based on three ontological universes of reference.
There are three universes, each of which is complete from within its point of view. From the point of view of a given universe, all other universes can be represented within it. The physical universe is composed of objects, some of which may be viewed as references to other objects. Certain collections of these references, viewed from a subjective point of view, are known as subjective universes. Within a subjective universe, there are references which constitute a conceptual universe (these references are called concepts). All things are parts of at least one of these universes. Depending on one's point of view, each thing may be assigned to a basic ontological level: either physical, perceptual, or conceptual.

Cognitive set theory is a model of cognition. The formalization of its operating principles relies in large part on mereology, set theory, and linguistics. Cognitive set theory can be grossly characterized as set theory with a mereological understanding of elements: it is a formal model which encompasses syntax and semantics. However, this characterization ignores several important differences:
-
Cognitive set theory is cognitive: its primary purpose is to describe cognition, as opposed to establishing a framework for mathematics.
-
References (such as concepts and symbols) are introduced in the language explicitly. To do so, the Zermelo hierarchy is reformulated as a two-stage, perceptual and conceptual process.
-
Dichotomy and collection are interpreted as functions of perception and conception, respectively. The notion of dichotomy is taken from mereology, and is similar to intersection (although it can be applied to continuous things). The notion of collection is taken from set theory, and is similar to union (although it operates on sets themselves, rather than on their elements).
-
There are no axioms related to infinity (infinity is neither affirmed nor denied: it is simply never encountered in practice).
-
The restriction to first-order logic is dropped, since it is not appropriate when modeling human languages.
-
Syntax and semantics are united under a multidimensional model of cognition, and are formalized in terms of set theory and mereology (respectively).
Set theory and mereology are logics which have complementary strengths and weaknesses. Set boundaries (or curly braces) prevent things like subset transitivity, and make things like intersection somewhat awkward. On the other hand, the tendency of mereology to fuse its parts together is problematic if we wish to keep the parts distinct (which is essential for references): mereology does not have the property of additivity. Cognitive set theory is a proposal for how these two logics can be brought together in a way that mirrors the operation of the mind.
The following sections informally introduce the concepts of universe, parts, and references, followed by a summary of some of the many points of connection with mereology and set theory. This is followed by a number of rules that describe the operation of cognition, which operate in terms of these universes and references. Finally, the relation of this model to logic and linguistics is discussed.
There exists a thing called a universe, U, which is unique. To differentiate it from other universes, it is sometimes referred to as the physical universe.
The universe is the largest thing, unique unto itself. Precisely because there is nothing else to compare it to, however, it makes little sense to speak of it as the largest , or even unique . These remedial terms are only appropriate if it is conceived of as not the largest or not unique . Everything can be divided, which results in parts: it can be divided perceptually or conceptually, regardless of its physical divisibility.
References refer to other things (which may themselves be references). The first equation above states that y is a reference to x . Another way of writing a reference to x is to add to it a single tick mark: x' . This indicates that the referential level of a reference is one higher than that of the thing to which it refers.
References refer to parts of a universe, as well as being parts of a universe themselves. When they are collected together and understood as references, as opposed to being merely things, they have the characteristic property of forming a referential universe. This referential universe is the collection of all references from a particular point of view. As references depend on a particular point of view, there are multiple subjective universes: for example, different animals have subjective universes (or, from their point of view, different animals are subjective universes).
The set theoretic formalism is particularly good for manipulating discrete quantities, but it is notoriously bad for manipulating continuous quantities. Although it is possible to overcome this deficit with various contrivances, the use of sets in cognitive set theory is restricted to that which they are most suited: discrete things (continuous things will not be discretized in order to apply set theory ubiquitously). The approach used here is to augment set theory, which is used for discrete quantities, with mereology, which is used for continuous quantities.
Mereology is similar to set theory, and was developed at approximately the same time. Although it is not as popular as set theory, it has undergone a good deal of formal scrutiny, and it is regarded to be a solid foundation for formal logic. It is particularly well-suited to spatial logics. Unfortunately, it has historically been viewed as a competitor to set theory, as opposed to a counterpart, so the historical popularity of set theory reduced the potential contribution of mereology.[106]
Mereology literally means the study of parts ( mere is Latin for part). As opposed to set theory, mereology is characterized as having a transitive parthood relation. For example, if x =pt( y ) and y =pt( z ), then we may infer that x =pt( z ). As previously mentioned, this is not the case for the set-theoretic element-of operator (for which transitivity is guaranteed not to hold).
Another way of seeing the distinction between sets and parts is to consider the combination of the sets { x }, { y } as opposed to the parts x , y . Suppose that x represents all people, and y represents all animals. The combination (or union) of { x } and { y } is { x }+{ y }: it does not reduce further. The combination (or fusion) of x and y , however, is merely y : since people are animals, adding the part of the world that constitutes humans to the part of the world that constitutes animals does not result in an increase: that part has already been counted. Set braces prevent this combination, because the set of people is not a part of the set of animals.
The parts of a universe are known as things , and are created from a larger whole using the pt() operator. The pt() operator is not intended to be unique: pti(x) is not equivalent to ptj(x), i.e. all parts are not equal. The first equation above states that there is a relation between two things, y and x , such that y is a part of x . The second equation, which assumes that Y and X are references, states that the thing which is referenced by Y is a part of the thing which is referenced by X .[107]
The notion of parts used here is that of proper parts: a part must be strictly smaller than the thing of which it is a part. The parthood operation is therefore a dichotomizer in that its operation always produces two non-empty parts (a part and its counterpart). This notion of dichotomy leads directly to the definition of negation.
Given some parthood operation, pt(), and a divisible thing x , it is possible to separate x into two things: pt( x ) and x -pt( x ). If x is known, these two concepts may be referred to as simply pt( x ) and ¬pt( x ), as in the first equation above. This may be rewritten as the definition of the negation operator, which is done in the second equation.[108]
Sets are often intuitively defined in terms of collections, elements, classes, etc. Although these may be valid characterizations, the most important point to emphasize from the perspective of cognitive set theory is that sets are concepts. As such, they are things that can be named (by words), and they are also references to percepts (which are in turn references to objects).
Sets themselves are atomic, although they may contain, or correspond to, a plurality of things. This dual behavior is made possible by the fact that they are (single) references to multiple things: they are atomic in the referencing domain, and plural (or at least potentially plural) in the referenced domain. This is indicated by the curly braces that are used to construct sets: these curly braces are ontologically significant, and constitute a boundary which is a discontinuity.[109]
The first equation above states that Z is the set containing x and y . The second equation states that Z is a reference to x and y . The first equation is understood in a cognitive context as saying that Z is a concept; as such, it is also a reference to x and y , which we may further assume are percepts. The curly braces which are used for the creation of a set are an alternative notation for the function which creates a reference (which we have called ref ). The advantage of using the functional form is that its inverse can be denoted relatively easily (which is not the case when using curly braces).
Sets are conventionally defined in one of two ways: either as a formula in a given language (the intensional definition) or in terms of the enumeration of objects which possess that property (the extensional definition). To express this in more psychological terms, concepts can be defined either with perceptual formulas or as collections of other concepts. Ultimately, all conceptual content is referential, and can be traced to perception. Mapping this to the theory of sets, it entails that all extensional definitions of sets in cognitive set theory must involve elements which ultimately have intensional definitions (this is related to the notion of well-foundedness).
The primitive of set theory is the element-of operator, which is denoted ∈. If a set Z consists of x , then x is an element of Z (this is shown in the first equation above). In contrast to set theory, cognitive set theory does not introduce the element operator as primitive: other operators are used to achieve the same operation. In particular, the effect of the element-of operator can be achieved by selecting a part of a dereferenced set: this is shown in the second equation, above.[110]
The element-of operation enables a simple definition of the subset operation. The two formulas above both express the fact that X is a subset of Y : they are similar to the previous mereological formulas in Equation 11.3, “Parts”, that express that X is a part of Y . The first equation states that X is a subset of Y , using the subset operator. The second equation defines a subset in terms of its elements, using first order logic: for all entities z , if z is an element of X , then z is an element of Y . It additionally states that X is not equal to Y , which makes X a proper subset.
To say that a thing is atomic is to say that it has no parts.
The definition of a universe entails that it is not a part of any other thing. It could alternatively be expressed as that thing whose complement is exactly nothing. This has historically been problematic for set theory, because it is easy to imagine things that contain this universe (in mereology, this is not possible). For sets to contain the universe, however, requires that references are formed in another universe (or in more set theoretic terms, the creation of that set happens in another level of the Zermelo hierarchy, where there is a different definition of U).
The empty set is a reference whose referent does not exist. A reference which does not refer to anything is known as nothing, or the empty set. Since nothing is unique, it is given a special notation: a zero which has been struck through.
A reference to the entire universe is known as everything, or a full set. Everything is denoted with an unbroken circle. A set which is a reference to a full set is also a full set, although it is a full set from a different perspective.
There are three universes which merit particular attention from the psychological point of view: the physical universe (U), the subjective universe (O), and the conceptual universe (V).
There exists a thing called the universe, U, which is unique. It is everything. To differentiate it from other universes which we will introduce shortly, it will sometimes be referred to as the physical universe. Parts of U are called objects.
A given subjective universe is defined as a reference (or set of references) to the physical universe (a full set). The part that is left over is called the objective universe (this objective universe is clearly relative to that specific subjective universe). Both of these terms may carry subscripts, since there are as many subjective universes as there are individuals.
The subjective universe is denoted with the letter O. The subjective universe is the universe as it is experienced on a subjective (or individual) level. From the subjective point of view, all perception, conception, and even the objective universe are contained in O. By definition, it is impossible for a given individual to perceive of anything outside of O. Parts of O are called percepts.
The third universe is the conceptual universe, which is a part of the subjective universe. It exists in the same relation to the objective universe as the subjective universe exists in relation to the physical universe. The conceptual universe is denoted with the symbol V. Parts of V are called concepts.
This section explores the four referential operations between the universes we have just introduced:
-
Perception maps from the physical universe into the subjective universe. It creates percepts, which reference objects. It is denoted with the psy operator as follows:
O ≜ Ψ(U) -
Communication maps from the subjective universe into the physical universe. It often entails the creation of symbols in the objective domain. It is denoted with the delta operator as follows:
U ≜ Δ(O) -
Conception maps from the subjective universe into the conceptual universe. It creates concepts, which reference percepts. It is denoted with the phi operator as follows:
V ≜ Φ(O) -
Naming maps from the conceptual universe into the perceptual universe: it creates symbols in the perceptual domain, which reference concepts. It is denoted with the epsilon operator as follows:[111]
O ≜ ε(V)
In the previous sections, the referential operators were primarily applied to universes to produce successive universes of reference. However useful, this is not the primary role of references: typically, references correspond to parts of a larger whole, not the whole in its entirety. Hence, subsequent analysis will be increasingly concerned with the relationships between parts of these universes of reference. Further, because these referential operations take place on known domains, we will often indicate a particular concept as a specialization of the referential operator, as opposed to a specialization of the domain on which it operates. For example, instead of writing Φ(oi) to indicate a given concept, we may write it as Φ i(O) (and since the domain is known in this case, even more concisely as Φ i).
The process of creating references to the physical universe is called perception. Perception is denoted by the operator Ψ, it operates on the the physical universe, U, and it informs a subjective universe, O. Perception projects the objective world into the subjective world. It can be thought of as a function which maps the world into a neuronal representation. Typically, it is constrained by attention: we perceive some part of the universe. The narrowing of perception that occurs with attention is modeled as function composition in the second equation above.
In the first equation, perception is represented as an operator which maps from U to the entirety of O (where we intend the subjective universe of exactly one individual). However, this is somewhat incorrect because the entire physical world is not available for an individual to perceive: the domain of perception is some local portion of the physical universe. Although this level of detail is omitted here, functions such as perception are composite operations that can be broken down further. If we assume that attention is responsible for guiding perception, a finer-grained model of perception can be modeled as follows:
For our purposes, the codomain of Ψ is modeled as a single, high-dimensional perceptual space: it has an associated measure, and it is isomorphic to the external world (assuming that our perception is valid). Although perception usually includes modal-specific percepts (such as vision and hearing), here we consider only the perception of these senses as combined in a single perceptual space.
Perceptual space is divided into percepts. Percepts are parts which may be characterized as N-dimensional volumes, the result of dichotomizing a larger perceptual whole. This perceptual dichotomization is nominal, in the sense that it does not result in changes to the physical world when it is applied; it is not intrusive on the thing which is dichotomized. In other words, the division exists in the referring domain only: the “dividing line” itself is not a part of either a thing or its complement.[112]
Perception is modeled as function composition, where the domain of perception is the Universe. This is depicted in the first equation, where functions operate on the input from earlier functions. Perception is order-dependent: although f(g( x )) may sometimes be equivalent to g(f( x )), order probably has a slight temporal effect if nothing else. In a linguistic context, such as modifying a noun with multiple adjectives, the order of the adjectives may not matter greatly. In that case, it is possible to model the combination of multiple perceptual operations (or parthood operations) as a mathematical product. Hence, the expressions listed above are equivalent, subject to the implicit presence of some spatial domain in the latter two formulations.
Dichotomy allows for the relatively arbitrary division of percepts: it can operate on percepts because they are spatial and continuous (or at least not atomic).[113] It is essentially a mereological version of intersection: it is different than the set-theoretic definition of intersection, which roughly entails breaking apart a set, choosing some of its members, and then putting them back in a set. In cognitive set theory, as mereology, those steps are explicit. Hence, the operation of dichotomy does not cross set boundaries: only dereferencing, the inverse of the original referencing operation, can deconstruct a set.[114]
Dichotomy can be interpreted as a dividing line which has a dimensionality of one less than the part which it divides. Hence, a line is divided by a point, a surface is divided by a line, etc. The dividing thing must completely divide the domain. If we take as the domain a plane which extends indefinitely in two dimensions, there are two possibilities for such a dividing line. One is a closed curve within that plane, and the other is an open curve that extends as far as that plane. Both of these curves are dichotomizers, because each of them completely bifurcates the domain.
It is essential to note that the dividing line is not a part of the space that it divides, as it does not take up any space in the domain which it divides. This is due to the fact that points are not seen as composing things, but as dividing them. Similarly, lines should be understood as cuts which divide a continuous plane: they are not things out of which that higher-dimensional continuum can be composed.
The conceptual universe is composed of references to the subjective universe: these references are called concepts. Concepts are modeled in this book with sets: the formation of a concept is functionally denoted by the operator Φ, and the understanding (or dereferencing) of a concept by Φ -1. As with sets, concepts are also represented using curly braces, {}.
A concept is a reference which is treated as an atomic entity, even though it may represent (i.e. refer to) something with parts. In other words, because a concept is both a set and a reference, it is treated as an atom in the referring domain , although it may refer to a continuous element (e.g. a percept) or a (discrete) collection of concepts. Although it is somewhat unconventional to speak of sets as atomic (since they are defined as collections of elements), it is certainly not uncommon to treat them as singular entities: this is exactly what gives them much of their expressive power.
The first equation above shows a concept which is a collection of three percepts. The second equation illustrates an alternate notation for the same concept.
As mentioned previously, the dichotomy operator cannot be applied directly to a concept because concepts make their contents atomic (their contents are temporarily opaque). Further, if it were to be applied to a symbol, such as “apple” , the result would be something like “app” , which is meaningless. In order to allow the formation of subsets, we must first dereference the concept (break apart the set), select certain of its perceptual parts, and then collect these parts into a set. Collection, on the other hand, can only be applied to percepts and symbols (not directly to concepts, as in standard set theory). The result of defining these operators in this way is that all dichotomization (perception) must happen before any collection (conception), unless those concepts are visualized (i.e. their meaning is extracted). This ordering has significant topological consequences which will be explored later.
Naming is defined as the association of a concept with an arbitrary percept: its name. Names, or symbols, are parts of the perceptual universe that represent concepts. Hence, their referential level is one higher than the concepts they reference, despite the fact that they are percepts. In virtue of the fact that naming and conception form a loop, percepts and concepts are bound up in mutual reference.
Given a part of the physical universe, it is possible to form a percept which is a reference to it. Given this percept, it is possible to form a concept which is a reference to it. Given this concept, it is possible to again form a percept which is a reference to it. Hence, percepts may reference two very different types of things: in order to distinguish percepts-which-reference-objects from percepts-which-reference-concepts, the latter are called symbols (or names). They are formed using the naming operator, as depicted in the equations above, instead of being formed by perception.
The naming operator has an inverse, whose use is crucial: if we could name concepts, but we could not understand concepts when given their names, names would be of precious little value. We denote this dereferencing operator as the inverse of the naming operator (although it is probably implemented as a separate neural association, since biological inverses pose a tricky implementation problem).
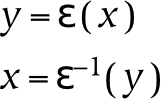
In the equations above, the naming operator creates a symbol, y , that references a concept, x . The inverse of this operation, which involves recognizing that symbol (i.e. re-cognizing or dereferencing), reactivates the meaning associated with that symbol. In English, the referencing or naming operation relies on the verb to be , as in the copula is or is-a . The dereferencing operation is similarly aided by linguistic constructs: for example, definite and indefinite articles can dereference a count noun, which makes it less abstract.
The outbound portion of communication entails the creation of objects in the world, such as hieroglyphs and sound waves. This communication may be symbolic or not, depending on the nature of what is being transmitted. If there is no symbolic content, communication may be treated exclusively as action (e.g. as in running). More often, communication is both an action (e.g. the movement of the lips, the movement of the hand) as well as the transmission of symbolic information (the words or the writing that result from this movement).[115]
The topological notions of connection and overlap are closely related to perception and conception. In particular, the operation of perception can be used to express connection fairly directly: by relying only on dichotomy, we can form only contiguous percepts. Hence, connection (or contiguity) can be defined as that which can be produced by (multiple operations of) dichotomy in a larger contiguous percept. To express overlap, it is necessary to add collection (since a part of a connected thing is always connected). In other words, in virtue of the way dichotomy and collection are defined, overlapping perception is not possible without introducing naming.
Two things x and y are connected if and only if they can be represented as a dichotomy of some larger connected (contiguous) z . That larger percept is contiguous because it is derived only from the repeated application of dichotomy to a universe, which is continuous by definition. In particular, that larger thing z must be formed without the use of collection (which would allow z to be a discontiguous entity). In more cognitive terminology, contiguous objects are the result of first perceiving everything, and then restricting attention to smaller parts of that percept (which can be modeled as multiple applications of perceptual intersection).
Two things x and y overlap if and only if they share a part in common (which is denoted as b in the equation above). Both overlap (and underlap, or discontiguous objects) require collection, since dichotomy alone forms only partitions. In other words, the limited scope of dichotomy and collection facilitate the definition of topological connection and overlap. The psychological implications of these topological definitions are somewhat interesting: a single percept must be connected. If overlap (or discontinuity) is required, then concepts (collection) must be used. Intuitively, this seems like a good result; perceptually, objects occlude one another, rather than overlap. Experimentally, this provides a number of testable hypotheses about perception of single and multiple things.
The ontological universes and the referential relations between them can be used to build increasingly abstract concepts. This abstractness can be quantified in terms of dimensionality. In other words, the following things may be collected into (separate) universes: all things, all things which are references, all things which are references to references, etc. Each of these universes consists of references with a different referential level, and each serves as the basis for a particular point of view.
The notion of conceptual order is similar to a concept's level of reference, although it tends to be more convenient. The level of reference of a concept increases with every reference: the order of a concept increases only when a thing is named. For example, if an object is a first-level reference, then a percept is a second-level reference, a concept is a third-level reference, etc. However, if an object is a first-order object, then a percept of that object remains first-order, as does a concept of that percept. It is only when first-order concepts are named that second-order things (symbols) are created. At the same time, the notion of conceptual order still provides a means by which to differentiate percepts that are symbolic from percepts that are not (i.e. percepts which reference objects are always first-order).
The order of a concept corresponds to the number of set braces used in the formation of that concept. The order of a concept assigns to each concept (or set) an integral index (first-order, second-order, etc) which corresponds to its level in the Zermelo hierarchy. There are a number of benefits associated with the Zermelo hierarchy, the most notable of which is that this correspondence goes a long way towards ensuring the well-foundedness of the system. Perhaps more importantly, this notion of order mirrors the way in which our concepts are formed: they are built out of pre-existing percepts and concepts.
The first equation above states that parts have a dimensionality which is equivalent to the wholes from which they are created. The second equation states that the dimensionality of a concept x'' is equal to the dimensionality of the underlying percept, x', in addition to any dimensionality added by the conceptual order.
Although the dimensionality of things in a given universe and the dimensionality of that universe itself are equivalent, universes do not necessarily have the same dimensionality as each other. For example, references often have a dimensionality which differs from the things they reference. Clearly, this is only true when they are understood as references: as parts, they exist in the same universe as the things they refer to, so in that context they necessarily have the same dimensionality as the things they reference.
The collection of multiple concepts enables an increase in dimensionality: the new dimension is a dimension of variation over the collected things. Since the things are atomic (as references), this collection is necessarily orthogonal to the things themselves: it is one-dimensional. Contrast this with a three-dimensional thing, which could only be combined with other three-dimensional things.[116]
There are two points of view with respect to the dimensionality of collected concepts. From one point of view, if each of the collected parts has a dimensionality of N, then by collecting them together, we have created a thing of dimension (N+1). From another point of view, as the collected things are atomic, the result is a one-dimensional collection. The difference between these points of view amounts to whether or not the concepts thus collected are dereferenced in the process of considering their dimensionality.[117]
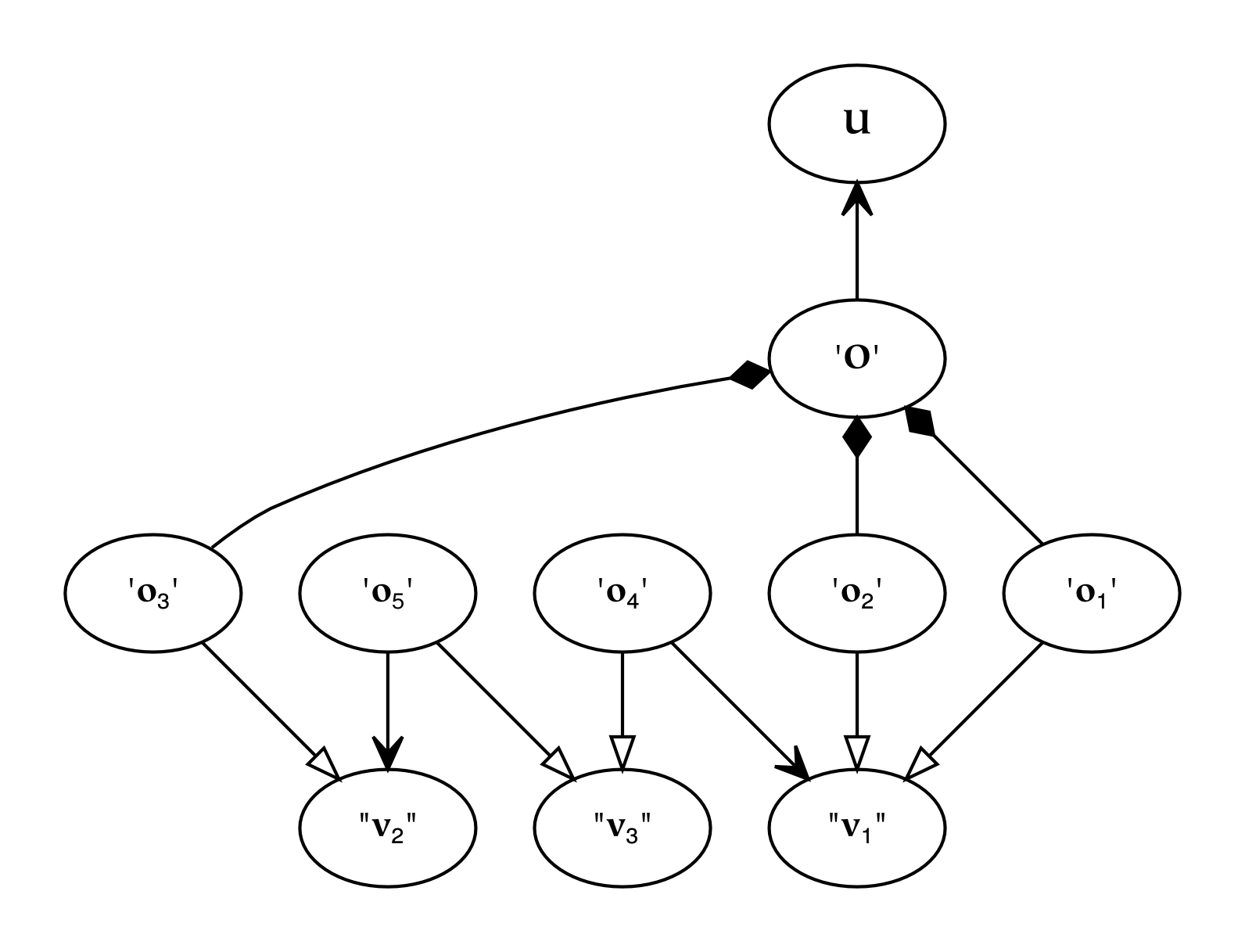
The diagram above shows several example relations between things in all three universes. At the top level, the Universe (U) is depicted: this is reflected into the perceptual universe (O), and subsequently divided into the percepts ‘ o1 ’ , ‘ o2 ’ , and ‘ o3 ’ . This perceptual hierarchy is a trivial example of a meronomy, or part-hierarchy (this is indicated by the diamond arrowheads). At the next level of the diagram, these percepts are referenced by the concepts “ v1 ” and “ v2 ” . These concepts unify their corresponding percepts, and each has a corresponding symbol or name: ‘ o4 ’ and ‘ o5 ’ . Finally, those names are collected into a single higher-order concept, “ v3 ” .
It is important to note that this diagram has deceptively clean lines: it is a misleadingly simple hierarchy, represented here with several symbolic nodes. While this simplicity is useful to visualize things, it is misleading in that the underlying implementation is distributed and considerably more tangled: it would have little resemblance to these pictures. However, this diagram does illustrate in a basic way how perception creates meronomies and conception creates taxonomies.
The process of creating a meronomy begins by partitioning a perceptual whole, which is represented in the middle two rows of the diagram above. Each part is produced by the operation of dichotomy (or partition). The process of creating a hierarchy is an iterative process of conception and naming, which is represented in the lower two rows of the diagram above. The dimensionality of percepts is not altered by creating parts, since many partitions are equivalent to a single N-way partition: dimensionality is increased by the creation of concepts, where percepts are collected at the bottom of the figure.
The conceptual hierarchy can be arbitrarily deep, although in the figure above there are only three concepts. The concept “ v3 ” is at the root of the conceptual taxonomy: although the existence of a single conceptual root is not necessary, it has an interesting correspondence to the perceptual universe (O).[118] It should be clear from the pictures that there are multiple ways to derive a concept such as “ v3 ” which ultimately corresponds to the perceptual universe (O). None of these derivations is more correct than another: although they may be expressed differently symbolically, they mean the same thing.
To understand this diagram better, we may give the nodes a familiar interpretation. Let us suppose that this diagram represents a world which consists of only one dog and one cat. We have not divided the physical universe into the dog and the cat; instead, we perceive the entire world, and we form concepts ( “ v1 ” and “ v2 ” ) based on seeing the dog once ( ‘ o3 ’ ) and the cat twice ( ‘ o1 ’ , ‘ o2 ’ ). Further, we learn the names for cat and dog ( ‘ o4 ’ and ‘ o5 ’ , perhaps ‘Felix’ and ‘Canus’ ). We think that Felix is something, and that Canus is something, but we do not have a word for that something (i.e. a name for the concept “ v3 ” ). If we were to name it, it would probably be something like ‘animal’ .
Identity is one of the most basic relations. In order to define identity, we begin with a situation in which nothing is identical with anything else: everything is unique unto itself. All perceptions are different: however, these different perceptions may be collected into concepts (and thus unitized). At that point, differences between individual percepts can be ignored or forgotten. It is in virtue of this forgetting that different percepts become identical (at least from the conceptual point of view).
There are several kinds of identity to consider, based on the relationship of different kinds of things to one another. For example, the identity conditions for parts are somewhat different than for references (at least when references are treated as references). We begin with the notion of identity between two things in the same universe.
Two objects within the same universe are identical (or are the same thing) if they are both intrinsically and extrinsically identical.
The equation of intrinsic identity states that two things are equal if and only if they are composed of the same parts.
The equation of extrinsic identity states that two sets are equal if and only if they are both parts of all larger wholes of which either one is a part.
Two references are referentially identical if they refer to the same thing. This entails that x and y are references, and that after some amount of dereferencing, they are identical to one another non-referentially. The notion of identity itself is not sufficient (as an identity condition) for references, because two different references are always different as things. On one hand, this outcome is desirable because we need a way to say that two references are not equivalent. However, we also need a way to say when references, which are not themselves identical, refer to the same thing (i.e. ref-1( x ) ≡ ref-1( y )).
Isomorphic identity establishes identity between references and the things that they reference (i.e. their referents). Isomorphic identity implies both extrinsic and intrinsic isomorphism. This entails that a reference is isomorphic to its referent if and only if both participate in the same extrinsic and intrinsic relations in their respective domains.
Isomorphism is guaranteed between a referential universe (a full set) and the universe to which it refers (at least when both things are regarded as undifferentiated). In other words, all full sets are isomorphic to one another: both their intrinsic and their extrinsic identity is trivially satisfied since they are both universes as well as atoms. For parts which are created from these universes, isomorphism requires structural similarity: a reference is isomorphic to its referent if everything of which they are parts are also isomorphic to each other.
George Boole's fantastic work entitled “The Laws of Thought” stated Aristotle's four syllogisms using the concise formulation shown above. In these equations, the letter v is used to express the concept of “some” (which we interpret as being synonymous with parthood), the numeral one (1) is used to represent truth, and zero (0) is used to indicate falsity. These laws have mereological counterparts which can be written in a straightforward manner as follows:
| Aristotelian Syllogisms | Mereological Equations |
|---|---|
| All y are x | y = pt(x) |
| No y are x | y = pt(¬x) |
| Some y are x | pt(y) = pt(x) |
| Some y are not x | pt(y) = pt(¬x) |
These mereological equations can be easily visualized with Venn diagrams. For example, the first statement (in which all y 's are x 's), can be represented as a circle around all of the y 's, inside of a circle around all of the x 's. All of these representations are mereological formalisms which are complementary to the existential quantification over individuals (i.e. we do not attempt to replace mereology with set theory).
Modern logic transforms the first statement above into the second statement with the use of existential quantifiers. As can be seen, existential quantifiers reduce abstract propositions to concrete propositions that range over (less abstract) individuals. While this is often a useful transformation, it cannot be the whole story from a cognitive perspective. A psychological version of set theory must allow direct expression of higher-order statements, i.e. statements which are not about individuals, but abstract things. Instead of using quantification over entities, which is a limitation imposed by first-order predicate calculus, abstract logical statements must be able to relate to one another directly. This is done in the third equation, which says that rectangles are types of polygons (where we have interpreted a type as an abstract part). In even more detail, rectangles are the part of polygons that are equilateral, which is expressed in equation four.
When it comes to expressing English in a formal language, the goal of logicians is not the same as the goal of psychologists. Logicians must be conservative with respect to the introduction of axioms. Psychologists, on the other hand, must respect the operating principles of the mind and the brain, even if those principles turn out to be somewhat redundant. For example, logicians might regard the sentence “Rectangles are polygons” as identical in deep structure to the sentence “Every rectangle is a polygon” , or even “Every thing which is a rectangle is a thing which is a polygon” . Although these statements may be logically equivalent under certain conditions, they are not equivalent from a cognitive point of view. For example, if quantification over all individuals were required to reach a conclusion, conclusions would take a good deal longer to reach.
If we allow for different cognitive structures corresponding to the sentences in the left-hand column, we might end up with the following table, where the order of the concepts involved in the relation is indicated in the third column:
| English | Cognitive Structure | Order |
|---|---|---|
| Rectangles are polygons | R ε P | second |
| Every rectangle is a polygon | ∀x : r(x) → p(x) | first |
| Every thing which is a rectangle is a thing which is a polygon | ∀x : x∈R → x∈P | first |
The quantification required by first-order logic relies on individuals and the existence of individuals. Hence, existential quantification works well for things which can be easily individuated, such as count nouns. It is awkward when applied to mass nouns, as in “water is wet” , where we are forced to read ∀w as “for all waters w” . Those concrete individuals must exist in order to be meaningful. This means that if there are no individuals satisfying the premise r( x ) in the second equation above (i.e. no rectangles), then the implication is true for the first-order sentences. On the other hand, the second-order version of the statement can be false even in a world without rectangles. In other words, actual rectangles are not required for the second-order formulation: we may infer the truth or falsity of statements from these second-order terms, independently of any individuals.[119]
The meaning of words derives from concepts, which in turn have a meaning that depends on the original contextual embedding of the percepts from which those concepts are ultimately formed. Syntax governs the combination of these semantic units; it is a referential calculus which organizes concepts in a high-dimensional space, and which provides a listener with rules to dereference the encoded meaning of various utterances by a speaker.
The deep structure of language and the study of syntax are crucial parts of cognitive set theory. However, there are two significant differences between cognitive set theory and syntactic structure. The first way in which cognitive set theory differs is with respect to its scope: by attempting to describe perception, and to a lesser extent reality, the modeling attempted in cognitive set theory extends beyond the range of syntax and semantics.
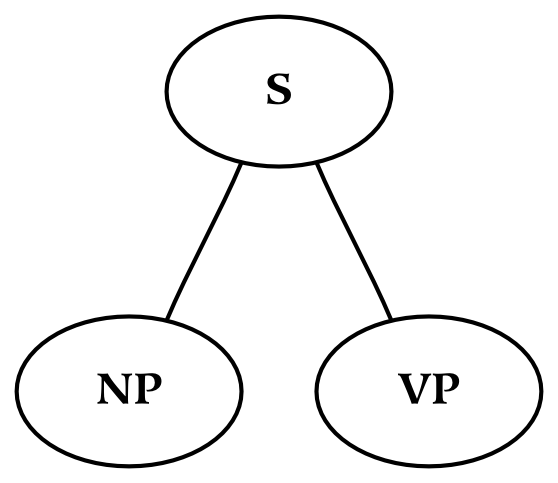
The second way in which cognitive set theory differs significantly from syntactic theory is that it recognizes two distinct kinds of syntax (or at least, an additional top-level production rule). These two types of syntax correspond to two types of sentences, those expressing an event and those expressing a relation. The first type is well-characterized by traditional binary-branching syntax and consists, at the highest syntactic level, of the combination of a noun phrase and a verb phrase. The second type of sentence creates an identity relation between two things (as opposed to constituting a reference to a thing). Although this second type of sentence arguably shares the same syntactic rules, is so radically different from other sentences at a cognitive level that it warrants a special treatment.
Consider the phrase “black cats” . Syntactically, this phrase is an adjective followed by a noun. Logically, both “black” and “cats” can be rendered with either properties (which the denoted entity has) or sets (of which the denoted entity is a member). The four possibilities for rendering this phrase are shown in the equations above. The first equation above is similar to the English sentence, where “cat” is a noun and “black” is a property. The second equation depicts “cat” as a property and “black” as a thing (a concrete individual). The third equation is especially amenable to an extensional set-theoretic interpretation, since it deals exclusively with entities and set membership. The fourth equation is expressed entirely in terms of properties: it is very close to a mereological formulation. A mereological point of view, however, does not need to quantify over entities, and may therefore be written as:
This rendering, precisely because it does not quantify over individuals, is what makes mereology such an attractive logic for dealing with shapes, substances, and other (potentially continuous) spatial things which do not come in neat and tidy (individualized) packages. It is attractive because it can be expressed without quantification (which has the side effect of dereferencing, or reducing the dimensionality, of the expression). In other words, by applying quantifiers to things ( there exists a cat, or the cat), we make those things more concrete (or less abstract). While this may be necessary in order to refer to things in the world, it is problematic given that our original phrase was “black cats” instead of “the black cats” .
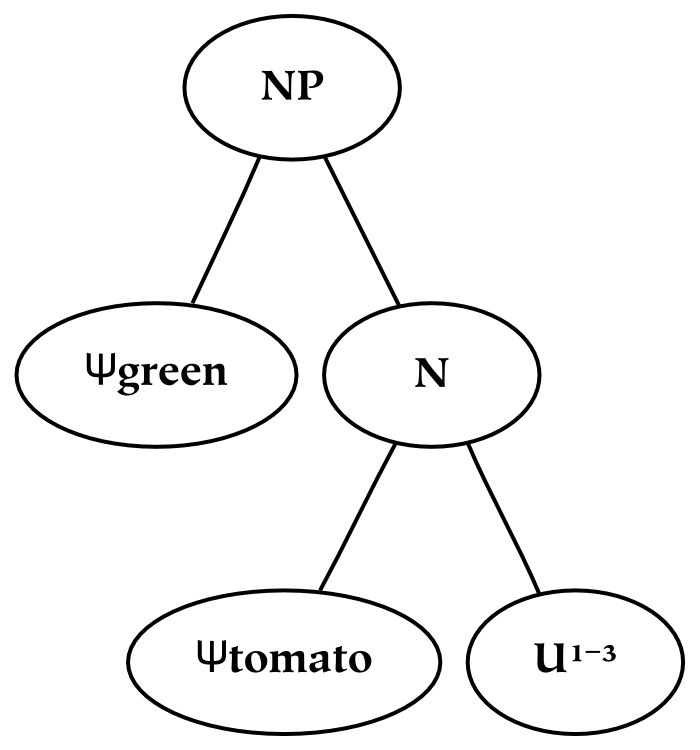
Nouns and adjectives are quite similar, despite the fact that they are different parts of speech: conceptually, “green tomatoes” and “tomatoey green-things” are approximately equivalent (at least denotationally). In both of these phrases, adjectives modify nouns: the English language requires a noun in subject position for proper interpretation. In cognitive set theory, the underlying cognitive structure of a noun essentially contains an adjective (this should be understood at a deep level, since it is clearly not true at the surface level). In other words, both nouns and adjectives are composed of the same cognitive operation. Nouns are essentially adjectives which have been applied (to space). Given this understanding, the cognitive structure of equation 11.34 can be represented as follows:
This structure illustrates that nouns are parts of speech which are themselves compound. For example, the noun “tomato” may be written as Ψ tomato(U 1-3), which may be understood in a manner analogous an adjective which has been applied to a space. Although treating nouns as pre-applied adjectives cannot be argued from the surface structure of English, this transformation simplifies the underlying cognitive processes. For one thing, having fewer cognitive structures than parts of speech is desirable, as it is unlikely that there are different mental mechanisms for all of the different parts of speech. By allowing the different parts of speech to share a common deep structure, they can be modeled in a uniform way. For example, just as noun phrases may be constructed out of adjectives and nouns, nouns themselves may be (implicitly) constructed from adjectives.[120] Similarly, verbs can be modeled as adverbs which have been applied to a conceptual space. As opposed to noun phrases, however, the conceptual space upon which verbs operate is time (U 4).
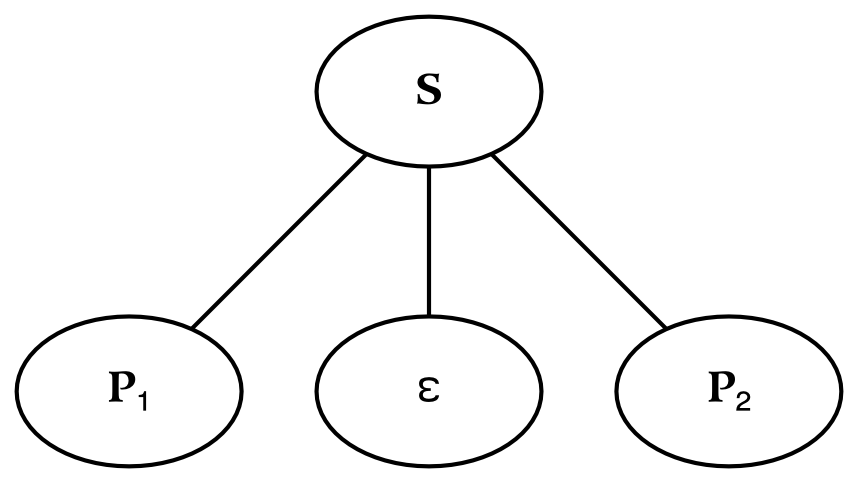
Statements which express a relation have their own production rule in cognitive set theory, which is depicted above. This is done to illustrate that these statements are categorically different from sentences using the production rule that divides a sentence into a noun phrase and a verb phrase. Even if syntactically we wish to preserve the traditional binary-branching tree structure, sentences expressing relations should be recognized as radically different from a cognitive perspective.
At a high level, the syntax of a sentence expressing a relation is modeled with three parts: a concept (such as the symbol which is to be defined), a copula (represented by epsilon), and a second concept (which provides the definition). Although there are numerous types of relations, all of them can be reduced to this ternary form. [121] The epsilon symbol is the relation that represents naming, and corresponds in English to some form of the verb to be . The operation of naming does not always introduce the name for the first time: it may only refine the definition of an existing symbol. However, in order to keep the presentation simple, we will consider the case in which the thing on the left is completely defined by (or becomes a name for) the thing on the right.
In order to illustrate the construction used to define new words, we consider the following phrase, where (D) represents “Dorsochimps” , (s) represents “small” , (m) represents “meddlesome” , and (a) represents “animals” :
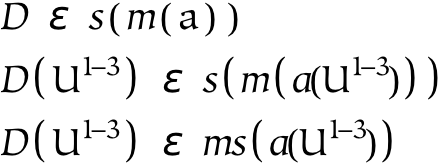
The symbolic formulation of the sentence is shown in the first of the equations above. In the second equation, the nouns are modeled in the same way as adjectives which have been applied to an (implicit) concept of space (which we have represented with the symbol U 1-3). Finally, in the third equation, intersection is used instead of function composition, under the assumption that the order of application does not make a significant difference for the adjective “meddlesome” . “Small” , however, must be understood in the context of animals, so it is not subject to this treatment.
An important characteristic of this sentence is that time does not enter the picture: this sentence expresses a relation between abstract entities. Even though this sentence possesses a verb, it is atemporal (or eternal), which is a common characteristic of relations. In other words, relations are independent of time, since they define abstract concepts. The ultimate result of this definition is the association of a new word (dorsochimps) with its meaning. This previously unknown symbol is tied to a single compound concept (using the operation of naming). A slightly more complicated definition would entail the collection of multiple concepts. For example, we might wish to say that dorsochimps are both small, meddlesome animals and things which often travel in packs (which requires the operation of collection).
In addition to sentences which express relations, there are also sentences which express things, or events in the world. As an example, consider a person reading the following sentence:
The apple from that tree probably tasted good.
This sentence is about the world. It is communicated as a series of symbols, so the underlying concept must be unpacked through successive operations of perception, conception, and understanding (the inverse of naming). Here we will conduct a basic syntactic analysis of the sentence to illustrate how it can be constructed as a single high-dimensional event.
At the first syntactic division, the sentence is a combination of a noun phrase and a verb phrase. The sentence structure can be broken down slightly further as follows:
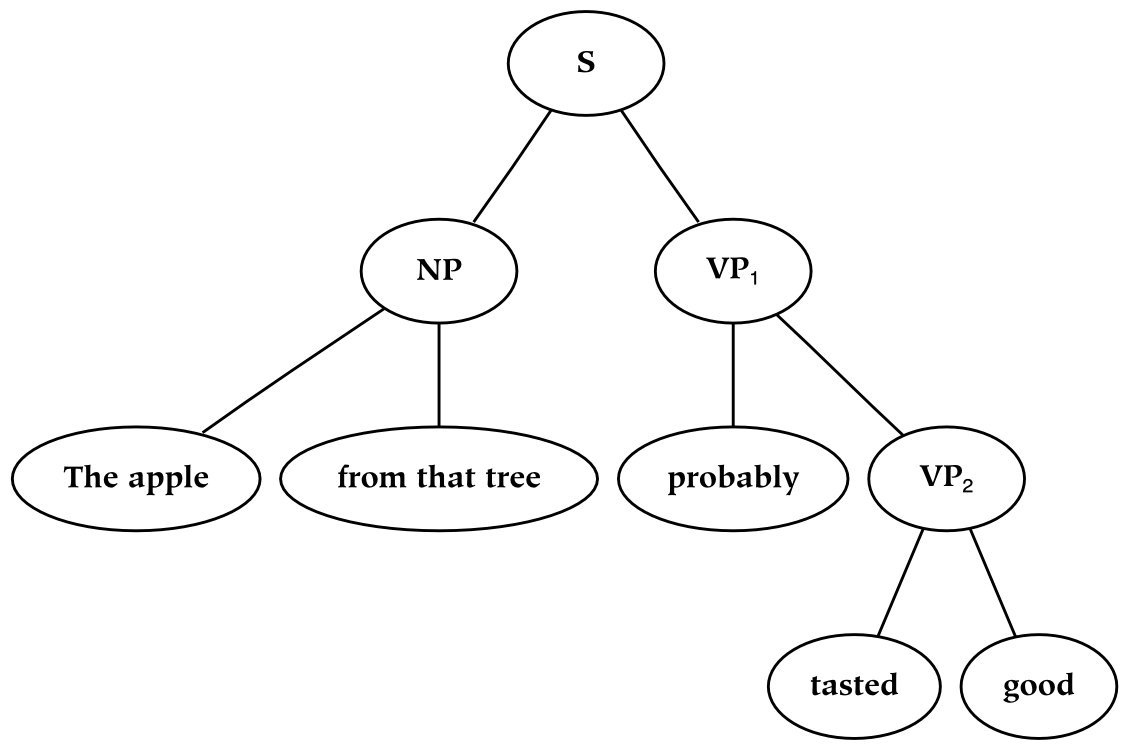
The noun phrase “The apple from that tree” is a dynamically-constructed concept (or an unnamed concept), as is every node in the tree during the process of its construction.[122] The subject of the sentence is “apple” : the apple is represented as an abstract count noun (a four-dimensional apple), which was at some point defined in terms of a number of individual apple concepts (each of which is a three-dimensional apple). The four-dimensional “apple-from-that-tree” is indexed by the use of the definite article. In so doing, the associated concept changes from an abstract count noun back to a dynamically-constructed concrete noun: the (three-dimensional) “ the -apple-from-that-tree” . The modification of the noun by the phrase “from that tree” does not alter the dimensionality of the thing, but it does refine the concept; it restricts the set of “apples” to the more restricted set of “apples on that tree” .
At this point, the concept corresponding to the (three-dimensional) noun phrase, the-apple-from-that-tree, can be joined with the verb phrase, “probably tasted good” . The modifier “probably” specifies the location of the thing on a modal dimension. In more philosophical terminology, of all of the possible and actual worlds, this modifier conveys that there is a significant probability that the thing which is being referred to occupies this world.
The rest of the verb phrase consists of a transitive verb and its object, “tasted” and “good” . The verb phrase adds a temporal dimension to the thing described; in this example, a previous time frame is indicated by the use of past tense.[123] The verb “taste” is itself abstract in virtue of the fact that it is transitive; it requires an additional part (the object of the sentence) before it can become a well-formed reference. In other words, “tasted-x” is a verb phrase which is itself essentially two-dimensional: the addition of the (required) modifier turns the verb phrase into a one-dimensional (temporal) concept.
The sentence refers to an object (i.e. a high-dimensional event). The constituent phrases each specify the nature of the object along different dimensions. The noun phrase is responsible for three spatial dimensions, and the verb phrase is responsible for modal and temporal dimensions. Collecting these together, we have a five-dimensional specification of a thing. In other words, the sentence is rendered as a five-dimensional event: three of which are spatial, one of which is temporal, and one of which is modal (i.e. associated with some probability of occurrence). This concept is communicated in written form. The process of communication entails the formation of the individual symbols corresponding to the constituent concepts, which are then communicated to the world through the inscription of the symbols on the printed page.
Through this communication, an object is created in the world: a series of typewritten characters. Although they are clearly a part of the physical universe and not concepts themselves, they have symbolic significance. The reader may retrieve the symbolic meaning from this perceived sentence through the reverse of the process just described. Critically important to this endeavor is to make the assumption that there is symbolic significance to the words that you are reading in the first place. You must believe that this inscription corresponds to a valid concept, otherwise you would be content to have merely perceived it, as opposed to having understood it.
[106] This story is changing, however: mereology is returning to the limelight of intellectual thought.
[107] Dereferencing a reference may result in multiple things : in this context, that would allow multiple entities on either side of the equivalence operator.
[108] In logic, the typical use of negation connotes that it is productive of a new truth. Since we view negation to be an inescapable result of dichotomy (or the parthood operation), it should be viewed as a method of referring to a pre-existing object. It is often used as a convenience to address the case in which we don't wish to name the object on both sides of a decision boundary. Its use implies that we know the domain of discourse: for logical operations, the domain of discourse is simply true or false. More generally, the negation operator can represent a mereological or set complement operation.
Sometimes the domain of discourse is implicit. For example, imagine the domain of “not fish” : it seems plausible that a bird is “not fish” , but it seems less plausible that the color green is “not fish” . In this case, the domain of discourse seems to be partially determined by the spatial characteristics of “not fish” .
[109] Failure to recognize this essential characteristic leads to a great misunderstanding of set theory. However, removing this boundary creates a logic closely related to mereology: from the mereological point of view, there is no difference between a thing and a part which contains all of that thing. In more psychological terms, there is no ontological reality to the set braces.
[110] One difficulty with the element-of operator (for our purposes) is that it is not constructive. We follow the convention of defining a left-hand side from a pre-defined right hand side, and we hold that elements must exist before a collection of those elements. Hence, the element-of operator cannot be used to constructively define new sets. It is perhaps unnecessary that the relation is constructive for mathematics, where it can be used simply as a relation. However, since we want to model cognition, and we view cognition as something which builds concepts out of other things, it makes sense to use only constructive axioms.
Unfortunately, the construction that we provide in the second equation is a bit more cumbersome than the equation which uses the element-of operation. However, this notational inconvenience is worth the benefit of an explicit (functional) formalism to represent curly braces.
[111] The use of an epsilon, ε, to denote naming is motivated by its use in the work of Lesniewski, where it has a very definite linguistic role (is-a). It should not be confused with the lunate epsilon (element) operation of set theory, or the extension operator of Hilbert. In fact, it is very similar to the inverse of Hilbert's epsilon (at one point in the writing of this book naming was written as a backwards epsilon, but that caused insurmountable typographical issues).
Lesniewski's system, called ontology, does not use sets, and set theory does not use the naming operator. In cognitive set theory, these two logical systems are conjoined by treating the following equations as synonymous:
[112] Topology finds itself in the awkward position of having to decide to which part of a divided whole the dividing line belongs. For this reason, cognitive set theory holds that the dividing line itself does not exist in the domain that it divides, much as a knife edge is not a part of the sandwich it cuts in half.
[113] We characterize percepts as continuous in light of the fact that they are continuous in comparison to concepts: whether they are ultimately continuous in a mathematical sense is somewhat irrelevant here.
[114] Although both continuous things and discrete collections can have a partition, atoms cannot. For example:
-
Continuous things can be partitioned, such as an apple or the percept of an ‘apple’ .
-
Discrete collections can be partitioned, such as coins (even if coins are atomic). Similarly, the collections of concepts (that represent these things individually) can be partitioned.
-
Atoms themselves cannot be partitioned: if they could, it would imply that the atoms had parts. Since concepts are atomic, the concept of an apple cannot be partitioned (without first casting that concept into a perceptual space).
[115] We are presuming that the physical universe is itself void of symbolic (referential) content, but that it may always be interpreted symbolically (referentially) by an observer. However, it may be the case that the world is never without meaning, in which case action without communication is impossible.
[116] It is an interesting question how dimensionality might be represented in the brain, because we have stated that the dimensionality of references is not equivalent to the dimensionality of the things which are referenced. Note that dimensional considerations are not an issue for concepts: since concepts are characterized as atomic entities, they do not have any dimensional constraints. The removal of these constraints allows concepts of arbitrary dimensionality to be collected in a one-dimensional space. The question of dimensionality is more interesting for perception, since the dimensionality of the world may be greater or lesser than the actual dimensionality of the representation in our brains, and perception maintains a (spatial) metric structure.
Neural encoding of dimensionality may be related to interconnectedness. For example, dimensionality can be approximately expressed as the number of neighbors shared by an atom: an element in a one dimensional space has exactly two neighbors, one to each side of itself on the line. Similarly, an element in a two dimensional space has four neighbors (assuming that neighbors are arranged in a Euclidean grid, and that one does not count the neighbors that can be reached diagonally). Following this line of thought further, an N-dimensional space can be produced by connecting each atom to 2N of its neighbors (in a regular fashion).
[117] We adopt the convention that concepts are always of a greater dimension than the percepts they reference (from a more mathematical point of view, we would say that the dimensionality increases, but the rank does not).
This convention is not a problem for collections, since there really is a dimension over which the individual concepts vary (i.e. the range of summation). For count nouns such as an apple, therefore, an increase in dimensionality will not come as a surprise: the formation of a count noun implies a concept with an extension that ranges over a plurality of instances. However, it is a bit puzzling for sets which consist of exactly one entity. Is a concept that corresponds to a single individual (i.e. the concept behind a proper noun) really of a higher dimensionality than the object which it names? Is it not just a reference to the latter? In this case, the dimension (even if it does exist) is not a proper dimension, but it is still treated as a dimension for uniformity with other (proper) dimensions.
[118] Note that “ v3 ” is not equivalent to the conceptual universe (V), which in this case would have to include “ v1-2 ” .
[119] It would be interesting to remove existential quantifiers entirely. For the existence operator, doing so is not difficult: for example, if we have a sentence such as “There exists a thing which is both a rectangle and a polygon” , we may render it logically as follows:
For the ∀ operator, however, this is harder to do. In particular, it is not clear how to remove quantification from the equations for intrinsic and extrinsic identity.
[120] Again, it is clearly not the case that adjectives are nouns, or vice-versa: they are very distinct things. However, nouns and adjectives share the same type of abstract cognitive operation in that they restrict space: adjectives are abstract because they have not yet been applied to a spatial entity, and nouns are concrete exactly because they have been applied to a spatial entity. In functional terms, the domain of adjectives is the noun, and the domain of nouns is space itself (although the latter is implicit in the English language).
We are not merely arguing that sharing a single cognitive implementation makes our lives simpler as psychologists. Reducing the complexity of the neural mechanisms which explain speech and language is justified in virtue of the fact that our brains, despite their enormous complexity, probably did not suddenly evolve lots of different mechanisms simultaneously to handle the different parts of speech. The ability to use most, if not all, parts of speech evolved more or less at once, so having only one underlying mechanism seems likely.
[121] Syntax decomposes sentences into noun phrases and verb phrases, while logic decomposes sentences into entities and relations. Logical relations are sometimes considered to be more powerful than binary branching syntax, but this is not the case. Expressions in either form can be re-written as expressions in the other: consider the relation “loves” in the phrase “Alec loves the girl” . Under a logical analysis, we may write this as follows:
Under a syntactic analysis, we may break this sentence into a noun phrase and a verb phrase:
On the surface, this sentence is different from the first sentence. However, this can be further analyzed into the following part structure, which is very similar to the first:
However, although these sentences can be transformed from one to the other, these transformations should be done with caution. These different structures may map onto very different meanings: we may view the fact that “Alec is a girl-lover” as a part of the definition of Alec, or as in “Alec currently loves the girl” (which is clearly a statement of affairs:).
[122] Although two concepts are not be able to be conceived at the same time, concepts can certainly occur successively, and two successive concepts whose names are known can be replaced by a concept which represents their union. Through this process, concepts can be created dynamically by successive union in a sentential hierarchy with a binary-branching syntax.
[123] In one sense, the verb phrase contributes a new dimension of analysis to the thing being conceived. On the other hand, if we consider a three dimensional thing to be really an unchanging four-dimensional thing, then we have not added any dimensionality, but have instead modified that unchanging thing (i.e. changed the shape of the object in the fourth dimension).