For two things to be called the same thing implies the notion of identity.
There are at least two criteria for identity. One criteria is bottom-up, according to which two things are the same thing if they are composed of the same parts. The other criteria is top-down, according to which two things are the same thing if they are parts of the same larger wholes. When references are considered, additional criteria must be introduced to establish identity conditions between different referential expressions, as well as the conditions between references and the things that they reference. The rest of this chapter looks at the concept of identity from these different perspectives.
Two things are identical when they satisfy all of the conditions for identity: both internal and external. However, these identity conditions entail that nothing is identical with anything else (things are only identical with themselves, and the world is full of either one or many unique individuals, depending on how one conceives of it). Therefore, it is necessary to loosen the conditions for identity in practice. In fact, knowing how these conditions should be loosened and how they should remain strict is exactly what constitutes learning the nature of things.
Knowing a thing's identity requires knowing the spatial boundaries of that thing.
Identity is defined spatially: to know a thing's identity requires knowing its boundaries (at a minimum). The spatial conditions are slightly different from the material conditions for identity, which says that things are the same if they are made of the same material. Another way of expressing material identity is to say that things are the same if they are made up of the same parts. A spatial notion of identity adds to this that things are the same if they are parts of the same larger wholes: it adds an extrinsic condition for identity.
In order to distinguish material and spatial identity, it is important to understand “being composed of the same parts” in a particular way. For example, although a car may be composed of a body and four wheels, it should not be understood only as the set of these parts: if that were the case, these parts may be randomly arranged and still constitute the same thing. The wheels, if they are stacked on top of the car, do not constitute the same object as the car in a more drivable configuration. In terms of parts, although both cars consist of wheels and a body, only one of these two configurations has a part which is axle-and-wheels (as a contiguous object). These cars are not the same in terms of their functional (extrinsic) relationships, either, since one of the cars will not roll down the road.
Most objects, or at least most objects that humans identify, possess clear spatial boundaries: a division can be made between an object and its environment which serves to delimit the object from what it is not. Although for many objects the boundary appears quite clear cut, boundaries are potentially quite complex. For example, knowing what an apple is requires knowing the boundary between apple and non-apple. At a macroscopic level, this is not too difficult: whether the stem or the leaf are parts of the apple is fairly easy to decide, at least in principle. At a microscopic level, it becomes less and less clear which parts belong to which object (for example, it is probably unclear to which object a given electron belongs).[36]
The objects that concepts refer to often stick together in space and through time: they are spatiotemporally contiguous. In some cases, this continuity of form may be very definite, like the shape of a diamond. In other cases, the shape may be more of a fluid connectedness, such as a puddle of water which is viewed as one thing, despite the fact that its shape may change greatly over its lifetime.[37] Some objects may even be discontinuous (although in this case, their status as singular objects is somewhat contentious). One example is that of an ant colony: from a linguistic point of view, an ant colony is singular. In terms of the objects which constitute that thing, the colony is composed of a plurality of ants.[38] However, the ant colony is also a single, concrete object, which just happens to be spatially discontiguous.
Knowing a thing's identity requires knowing the temporal boundaries of that thing.
On the one hand, time should be regarded as simply a fourth spatial dimension. On the other hand, since time is so cognitively different than the other (spatial) dimensions, it is worth treating separately.
Now we are reading a page. Now , a second later, are we reading the same page? Although it is slightly different than it was just a moment ago (it has different atoms, a different molecular arrangement, and has been read once more, etc), we would still conventionally say that we are looking at the same page. The debate over what exactly constitutes identity through time is an old one: maintaining strict requirements for temporal identity led Xenophanes, a citizen of ancient Greece, to state:
You cannot step into the same river twice.
One of the more famous puzzles pertaining to the notion of identity also comes from Greece, and is called “the ship of Theseus” .[39] The puzzle begins with the following conditions:
1. At one point and time, Theseus had a ship.
At this point, we know what Theseus's ship is (or at least we think we do).
2. The gods didn't like Theseus much, and as a result, his ship had to be repaired quite frequently.
At this point, even though some pieces of the boat have been replaced, most people have no hesitation saying (and believing) that it is the same ship.
3. Eventually, every piece of the original ship had been replaced.
At this point, the question of whether this is the same ship is a bit more difficult to answer. Most people probably maintain that it is still the same ship. However, it contains none of the original matter; all of the wood is different wood. If we maintain that the ship is the same, then we must be using criteria other than material criteria; we must believe that being composed of the same stuff is not a necessary condition for identity.
4. Theseus' evil twin, Feceus, collects all of the original pieces and builds a ship from these pieces.
At this point, there are two ships: but which of the two ships is the real ship of Theseus? Is one, or the other, or neither, or both, the ship(s) of Theseus? This uncomfortable choice might lead us to tease apart the concept of the ship of Theseus into two concepts: the same-material ship and the enduring-shape ship. If we do not tear our original concept apart (just as the gods tore apart the ship itself), we must settle for a rather one-sided view of things. Further, in case we think that the question about the identity conditions for a boat are irrelevant, we might consider other objects whose material is similarly swapped out (such as the cells of our body, which are supposedly replaced every seven years).
Given the large number and kinds of conditions for identity, it seems misconceived to form a rigid concept of the enduring, single, ship-of-Theseus. This example illustrates at least two good (and separable) criteria: being composed of the same material and the persistence of shape. Functional similarity is another popular criterion: the ship of Theseus may be defined as any ship that Theseus happens to own or sail on at a given time. There are many others, which points to the fact that any single criterion seems to be lacking.
Concepts which reference (or apply to) their object in an all-or-none fashion, such as being a particular boat, are made even more black and white by simple, rational identity criteria. This binary logic which dictates whether or not a concept applies to an object often does not correspond very well to the underlying reality of the situation. The change in underlying processes is relatively continuous, so our attempts to deal with these processes conceptually often results in rigid (or discrete) approximations.
Again using an apple as an example, we might ask: when did the apple begin? It was probably “not an apple” when it was unmixed flower and pollen. Even after these two mixed, most people would still not call it an apple. Does it instantaneously become an apple when there are 2, 4, or 8 cells? It seems problematic to hold that there is no apple, and then, at some instant in time, there is an apple. One alternative to defining this precise instant of creation might be to apply fuzzy temporal borders to concepts. In other words, the pollinated flower is not very much an apple, but it is somewhat an apple. As the apple develops, it becomes more of an apple; when it is ripe and ready to eat, is so much of an apple that we simply say it is an apple: one-hundred percent. In this case the apple, just before it was an apple, was not a non-apple; it was somewhat of an apple. Of course, fuzzy object boundaries do not make all of the issues involved with identity disappear; they just make those issues fuzzy, too.
The uncertainty at the beginning of the apple's existence is similar to the uncertainty at its end. If the apple falls off the tree and slowly composts, it does not cease existing as an apple at a given instant. This process may happen rapidly, but it does not happen instantaneously. It tends to become less and less of an apple until it is indistinguishable from the ground; or at least until it becomes something else. Perhaps it is not a coincidence that things tend to go out of existence when there is another category or word to which they belong a little better. For example, if we had a single word for “rotten apple” (e.g. rapple), it seems likely that apples would be doomed to live less long than they do now: they would cease to exist as soon as they became rapples (although of course, some people would argue that we would create the term “rapple” precisely because we recognized such an object in the world).[40]
To summarize, the beginning and the end of an object in the world often seem relatively continuous (at least up to the quantum level). Our percepts of the object are crude approximations of this underlying continuity (as neurons are much larger than subatomic particles). By contrast, the beginning and end of a concept are even more discrete. Although the sharp transition at the entry to or exit from a concept can be softened with various linguistic hedges, concepts most often either apply to an object or do not apply . Under this condition, it seems that categorization leads to categorical understanding, even if the objects so categorized are not inherently categorical things.
Two references are referentially identical if they have the same referent.
A single thing may be described on many levels, all of which are equally valid. For example, here are several descriptions of an apple, given by people in different lines of work:
-
Sociologist: “The apple is a kind of food-stuff to be fed to the masses by the proletariat to keep them from revolting.”
-
Psychologist: “The apple often stops the hunger neurons from firing, thus contributing to the cessation of the apple-gathering response.”
-
Biologist: “The apple is a fruit, whose sweetness has been selected by evolution to provide for the disbursement and fertilization of the tree's dicotyledonous progeny.”
-
Chemist: “The apple is a complex of medium-chain, starchy hydrocarbons. It contains approximately twenty grams of fructose.”
-
Physicist: “The apple contains primarily carbon, hydrogen, and oxygen. It warps spacetime in virtue of its mass.”
These statements are contrived to indicate that the nature of the apple depends on the observer's perspective. They indicate that the apple is defined by the relations into which it enters, and illustrate several of an unlimited number of these relations as emphasized by people in different professions. These different levels of description do not require different observers; they could be descriptions made by a single observer at different times. The observer-when-hungry will categorize the apple as something to eat (a sweet fruit); the same observer might later categorize the apple as something on which to do experiments (an uncomplaining test subject). These different levels of description are not necessarily exclusive of each other: they are just different points of view, each of which uses its own terminology. In practice, however, it is difficult to conceive of different points of view at the same time.
A reference has a valid correspondence to a referenced thing if their respective relations in each universe are identical.
Identity conditions have been given for both things which are not references and things which are references. But what are the conditions under which references correctly apply to the things to which they intend to refer?
Clearly, strict identity conditions are not adequate: as examined in the last section, even two references to the same thing are not identical. References and the things to which they refer are different in kind: the concept of apple is not at all like the object apple. Even references to references are somewhat different than references to objects. On the other hand, the concept of apple does not apply to the object of orange, so there are also clearly valid and invalid mappings between these two things.[41]
Subjective references are identical to their referents in virtue of the mathematical concept of isomorphism. Isomorphism comes from the words for “same” (iso) and “shape” (morph). If concepts are represented with tree structures, this term can be understood as a graph isomorphism: a reference correctly maps to a thing if and only if that reference occurs in the same position in a tree of references that the thing occupies in a tree of referred-to things. For example, consider the relative conceptual position of “apple” in the diagram below:
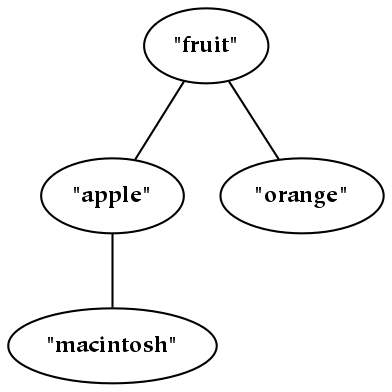
If the world of fruit corresponds to this picture (which might be verified through observation and talking to other people), then the concept “apple” and the object apple are isomorphic: we can validly impose a structure on the world that resembles this structure, even if the nodes in each domain are composed of entirely different stuff. In other words, because isomorphism is the only requirement, it is not necessary to have any relation other than congruence between objects and concepts: the concept of green does not require any intrinsic resemblance to a green object.
Just as with spoken language, in which arbitrary words can be associated with arbitrary concepts, random collections of neurons can map to arbitrary things in the world. The reference itself does not need to intrinsically correspond to the form of the thing to which it refers: only the relationships into which it enters must be the same. In fact, even the nature of the referential space may be different than the nature of the referenced space. For example, the referential space may be discrete, even though the space which is referred to is continuous.
[36] To further cloud the issue, recent physics experiments have shown that some properties of one object are instantaneously affected by altering an object at some distance from the first object at the level of very small particles. Although there are several ways in which to explain this finding, some physicists simply deny the independence of these entwined objects. In other words, they maintain that there is one object, which has spatially distributed components.
[37] Spatial boundaries, although they are fairly easy to identify, may not be the essential boundaries of a thing. W.V.O. [ Quine ] uses the example of a cat named Tibbles, whose boundary initially seems quite well-defined. However, if through some incident Tibbles' tail is cut off, then it is not clear if both parts are Tibbles, or if Tibbles refers only to the cat part and not the tail part (in the latter case, the tail was a nonessential part of Tibbles).
[38] Another (perhaps more convincing) example is a supercomputing cluster with wireless Ethernet connections. The cluster is in some sense a singular machine, potentially computing a single function, using hardware which is connected only by the transmission of information.
[39] Theseus was a sailor from Greece whose ship was repeatedly smashed by the gods.
[40] This example is similar to Zeno's paradox of the heap: if one has a heap of sand, and grains are removed one at a time, at what point is the heap no longer a heap? It seems counterintuitive to say that a single grain of sand can make the difference between a heap and a non-heap. If we conclude that a single grain of sand does not make the difference, we probably think of “heaps” as concepts which can apply to the things they describe to a greater or lesser degree, as opposed to being strictly binary predicates.
[41] References and the things to which they refer occupy different (referential) universes. The relation between references and the things that they reference is one of the bigger topics in philosophy: it is often encountered during discussions of dualism and qualia. Dualism (and monism) is a discussion about how the physical world relates to the mental world, and qualia is a discussion about the subjective experience of phenomena.